


C/C++培训
达内IT学院
400-996-5531

在C++编程的工作中,排序应该是常见的操作了,虽然在项目开发中需要我们手动实现的几率很小,但毕竟语言类库中都有很多种关于排序算法的实现。对于这方面的提升对我们C++程序开发者来说还有多有益处的。那今天说到的浅谈数据结构-选择排序(简单、堆排序),也是小编在C++培训课程的笔记中整理所出,希望对大家有所帮助!那我接下来看下一下!
选择排序:每趟从待排序的记录中选出关键字最小的记录,顺序放在已排序的记录序列末尾,直到全部排序结束为止。
选择排序正如定义所讲,在数组查询出最小值,然后放在此次循环开始位置(前一次循环已经获取比它更小的值放在前面)。
简单选择排序就是单纯的从数组中一次一次循环获取到最小值,放到循环位置。而堆排序正如名字,是从一个堆中选择,然后放在堆的循环开始位置,所以重点就是如何争取获取堆(分组)。
一、简单选择排序
1、算法思想
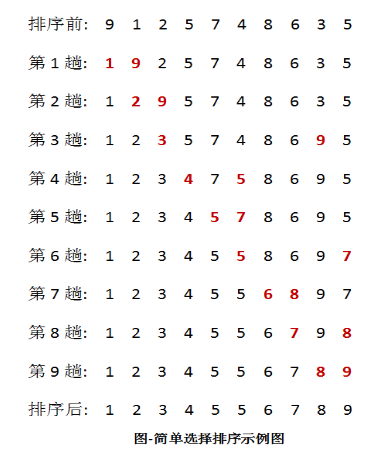
正如图上所示,每次选择最小值,然后放在本次循环的开始位置。
2、代码
//选择排序
void SortAlgorithm::SelectSort(pSqlList pList)
{
int i,j,min;
printf("开始验证选择排序");
//选择排序和低级冒泡排序很像,关键就是在比较时,低级冒泡进行数据交换,而选择排序进行记录,最后只交换一次
for (i =0;i<pList->length;i++)
{
min = i;
for(j = pList->length-1;j>=i;j--)
{
//注意数组坐标,千万别溢出
if (pList->SqlArray[min] > pList->SqlArray[j])
{
min = j;
}
}
//最后进行交换,先选择最小的,最后一次交换
swap(pList,i,min);
PrintSqlList(pList);
}
}
简单选择排序算法海华丝比较简单,关键点就是遍历寻找最小记录,然后入循环开始位置进行交换。
二、堆排序
1、堆排序概念
堆排序是首先引入完全二叉树的概念,就是构建完全二叉树,前提是完全二叉树是有特点的,也就是大根堆和小根堆。
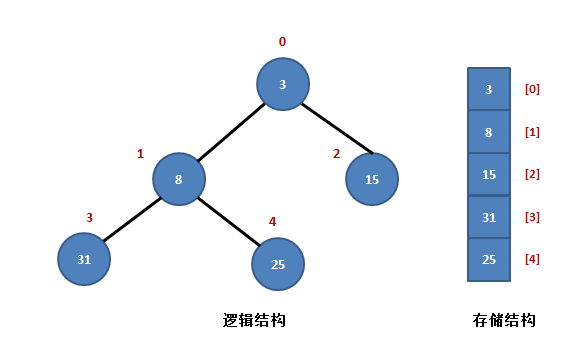
上图是完全二叉树,在完全二叉树中有几个性质:
设当前元素在数组中以R[i]表示,那么,
(1) 它的左孩子结点是:R[2*i+1];
(2) 它的右孩子结点是:R[2*i+2];
(3) 它的父结点是:R[(i-1)/2];
(4) R[i] <= R[2*i+1] 且 R[i] <= R[2i+2]。
大根堆:每个结点的关键字都不小于其孩子结点的关键字。
小根堆:每个结点的关键字都不大于其孩子结点的关键字。
2、算法思想
(1)根据初始数组去构造初始堆,默认是大根堆(构建一个完全二叉树,保证所有的父结点都比它的孩子结点数值大)。
(2)每次交换第一个和最后一个元素,输出最后一个元素(最大值),然后把剩下元素重新调整为大根堆。
上述算法是个循环操作,先构建,然后交换输出,最后调整余下的为大根堆,其实就是寻找最大值,其实只需要左右两个结点,那个比较大,就获取那个,所以调整堆排序也是比较简单,就是比较左右结点,获取最大值
第一步:构建大根堆
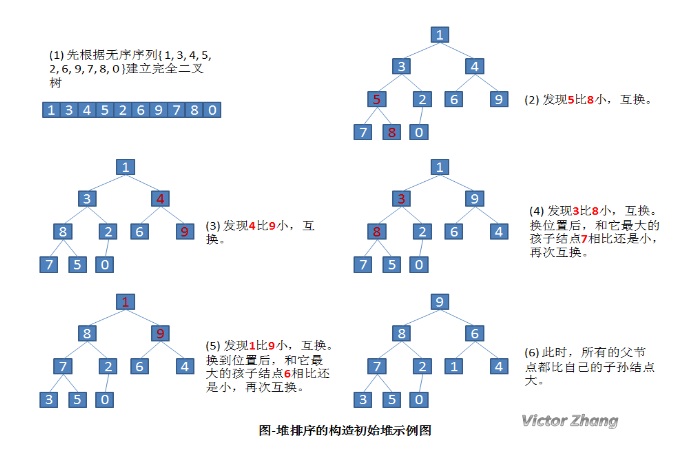
第二步、输出、调整

3、代码
////堆排序
void SortAlgorithm::HeapSort(pSqlList pList)
{
//循环构建堆
for (int i = pList->length/2;i>0;i--)
{
AdjustHeap(pList,i,pList->length-1);
}
PrintSqlList(pList);
for (int i = pList->length-1;i>1;i--)
{
//循环输出根节点,同时再次调整为大根堆
swap(pList,1,i); //根节点位于最前面,也就是1,这样就将1最大值,放在数组后面了
AdjustHeap(pList,1,i-1);
PrintSqlList(pList);
}
}
inline void SortAlgorithm::AdjustHeap(pSqlList pList,int start,int length)
{
int temp = pList->SqlArray[start]; //这是分支节点,然后比较它的分支节点,也就是2i
for (int i = 2*start;i<length;i = i*2)
{
//获取左右结点中比较大的值的坐标
if (i<length && pList->SqlArray[i] < pList->SqlArray[i+1])
{
i++;
}
//如果根节点本来就大,无序调整
if (temp > pList->SqlArray[i])
{
break;
}
//交换值,将左右结点大值放在根节点
pList->SqlArray[start] = pList->SqlArray[i];
start = i;
}
//将开始需要比较的值,放在最后交换出的位置上
pList->SqlArray[start] = temp;
}
4、代码分析
程序中一开始构建,调整大根堆,最大值是length/2,因为从完全二叉树的概念上分析:
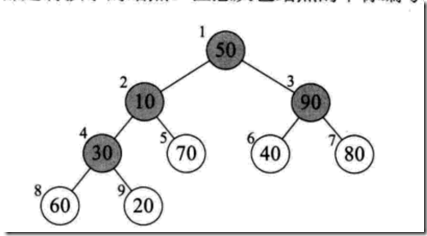
在上图中大根堆的建立,就是调整前四个元素的位置,就是放再分支节点上还是叶子结点上,所以只要输入4即可。
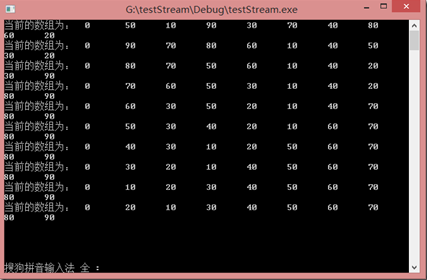
一开始大根堆,发现是90在最前面。
首先,将位于第一位(根节点树最大),然后和最后一位交换,然后调整前8位(第九位已经是最大了)。
然后,再讲获取到的80,和最后一位(第九位,第十已经不需交换),然后调整前7位,当然都是从1开始了。
最后经过一次次循环调整,完成算法的排序。
其中关键的思想是获取调整堆排序,比如一开始90和20交换后,20位于第一位置;此时20和左右结点中的较大值80交换,关键是后续继续拿20和后面左右结点比较,直到break,也就是找到比它小的,跳出,然后赋值。
三、性能分析
1、简单选择排序
从简单选择排序的过程来看,它最大的特点就是交换移动数据次数相当少,这样也就节约了相应的时间。分析它的时间复杂度,无论最好最差的情况,其比较次数都是一样多,第i趟排序需要进行n-i次关键字的比较,此时需要n-1 +...+1 = n(n - 1)/2次。而对于交换次数而言,当最好的时候,交换次数为0,最差的时候,也就初始降序时,交换次数为n-1次。总的时间复杂度依然为O(n2)。
尽管简单选择排序与冒泡排序同为O(n2),但简单选择排序的性能上还是要优于冒泡排序的。
2、堆排序
堆排序是一种不稳定的排序方法。
因为在堆的调整过程中,关键字进行比较和交换所走的是该结点到叶子结点的一条路径。
在程序运行时主要消耗在初始化构建堆和重建堆的反复刷选上。在初始化构建堆时,是从非终结点开始,其实比较两次,本来时n/2,这样最多对n/2进行两次比较工作,所以初始化构建大根堆是O(n)。
在调整构建堆时,第i次构建树logI(根据完全二叉树性质),需要遍历N-1记录,所以时间复杂度是O(nlogn)
以上尽是数据结构-选择排序(简单、堆排序)的进本讲解内容,达内C++培训班新一期又在招生中哦,同学们如果有兴趣欢迎你们的垂询。
免责声明:内容和图片源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容
Copyright © Tedu.cn All Rights Reserved 京ICP备08000853号-56  京公网安备 11010802029508号 达内时代科技集团有限公司 版权所有
京公网安备 11010802029508号 达内时代科技集团有限公司 版权所有