C/C++培训
达内IT学院
400-111-8989
C/C++培训
c++程序员面试 - 二叉平衡树的插入
平衡二叉树(Self-balancing binary search tree)又被称为AVL树(有别于AVL算法)，且具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。
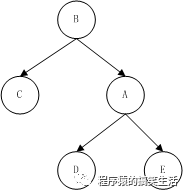
如下图示一个平衡二叉树：
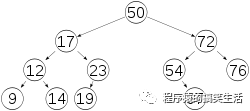
1. 左旋和右旋：
左旋：以A为中心逆时针旋转，实际就是：把B移到A的位置，把B的左子树作为A的右子树，再把A变成B的左子树。在平衡树种以平衡因子为-2的节点为中心做左旋操作。
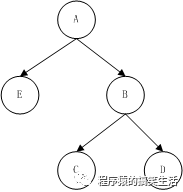
左旋前
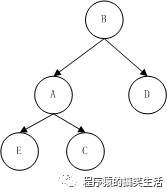
1. /左旋
2. void RotateLeft(tNode** root)
3. {
4. tNode * p=*root;//相当于A
5. tNode* lc=p->pright;//相当于B
6. tNode* llc=lc->pleft;//相当于C
7. p->pright=llc;
8. lc->pleft=p;
9. *root=lc;
10.}
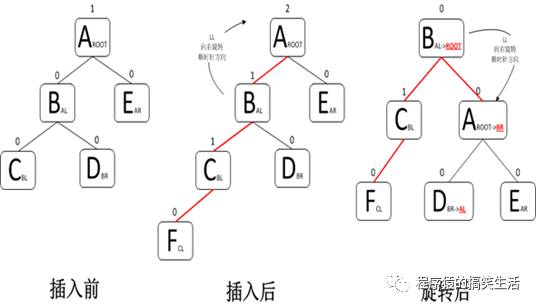
右旋：以A为中心顺时针旋转。实际就是把B移到A的位置，把B的右子树变为A的左子树，在把A作为B的右子树。在平衡二叉树中以平衡因子为2的节点进行右旋。
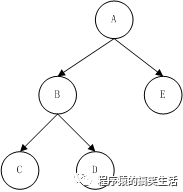
右旋前
右旋后
1. void RotateRight(tNode** root)
2. {
3. tNode* p=*root;//图中相当于A
4. tNode* rc=p->pleft;//相当于B
5. tNode* rrc=rc->pright;//相当于D
6. p->pleft=rrc;
7. rc->pright=p;
8. *root=rc;
9. }
平衡二叉树的插入时的四种不平衡情况：
(1)“左左”
由于在A的左孩子B的左子树上插入结点F，使A的平衡因子由1增至2而失去平衡。故需进行一次顺时针旋转操作。即将A的左孩子B向右上旋转代替A作为根结点，A向右下旋转成为B的右子树的根结点。而原来B的右子树则变成A的左子树。
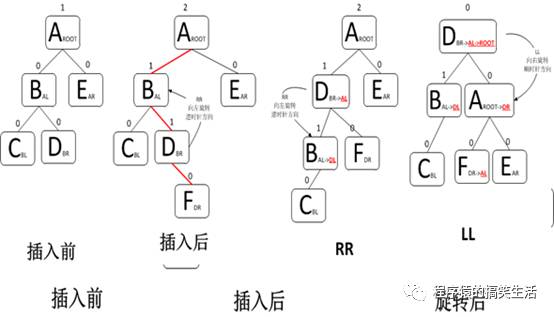
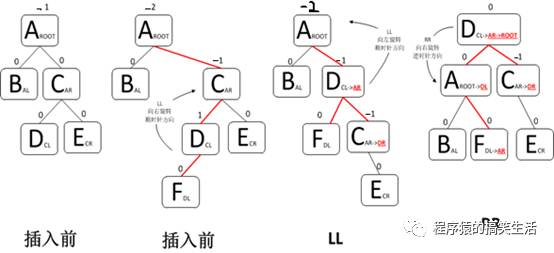
(2)“左右”：
由于在A的左孩子B的右子数上插入结点F，使A的平衡因子由1增至2而失去平衡。故需进行两次旋转操作(先逆时针，后顺时针)。即先将A结点的左孩子B的右子树的根结点D向左上旋转提升到B结点的位置，然后再把该D结点向右上旋转提升到A结点的位置。即先使之成为LL型，再按LL型处理。
插入代码：
1. void LeftBalance(tNode** root)
2. {
3. tNode* p=*root;
4. tNode* c=p->pleft;
5. tNode* rc=c->pright;
6. switch(c->bf)
7. {
8. //LL情况
9. case 1:
10. {
11. p->bf=c->bf=0;
12. RotateRight(root);
13. break;
14. }
15. //LR情况
16. case -1:
17. {
18. switch(rc->bf)
19. {
20. case 1:
21. {
22. c->bf=0;
23. p->bf=-1;
24. break;
25. }
26. case 0:
27. {
28. c->bf=0;
29. p->bf=0;
30. break;
31. }
32. case -1:
33. {
34. c->bf=1;
35. p->bf=0;
36. break;
37. }
38. }
39. rc->bf=0;
40. RotateLeft(&c);
41. RotateRight(root);
42. break;
43. }
44. }
45.}
(2)“右右”：
由于在A的右孩子C的右子树上插入结点F，使A的平衡因子由-1减至-2而失去平衡。故需进行一次逆时针旋转操作。即将A的右孩子C向左上旋转代替A作为根结点，A向左下旋转成为C的左子树的根结点。而原来C的左子树则变成A的右子树。
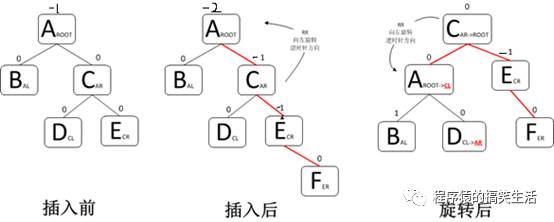
“右左”：
由于在A的右孩子C的左子树上插入结点F，使A的平衡因子由-1减至-2而失去平衡。故需进行两次旋转操作(先顺时针，后逆时针)，即先将A结点的右孩子C的左子树。
1. void RightBalance(tNode** root)
2. {
3. tNode* p=*root;
4. tNode* c=p->pright;
5. tNode* lc=c->pleft;
6. switch(c->bf)
7. {
8. //RR情况
9. case -1:
10. {
11. p->bf=-1;
12. c->bf=0;
13. RotateLeft(root);
14. break;
15. }
16. //RL情况
17. case 1:
18. {
19. switch(lc->bf)
20. {
21. case 1:
22. {
23. p->bf=0;
24. c->bf=-1;
25. break;
26. }
27. case 0:
28. {
29. p->bf=0;
30. c->bf=0;
31. break;
32. }
33. case -1:
34. {
35. p->bf=1;
36. c->bf=0;
37. break;
38. }
39. lc->bf=0;
40. RotateRight(&c);
41. RotateLeft(root);
42. break;
43. }
44. }
45. }
46.}
本文内容转载自网络，本着分享与传播的原则，版权归原作者所有，如有侵权请联系我们进行删除!
预约申请免费试听课
填写下面表单即可预约申请免费试听！怕钱不够？可就业挣钱后再付学费！ 怕学不会？助教全程陪读，随时解惑！担心就业？一地学习，可全国推荐就业！
-
扫码领取资料
回复关键字：视频资料
免费领取 达内课程视频学习资料
-
搜索抖音号搜索抖音号：1821685962
免费领取达内课程视频学习资料
Copyright © Tedu.cn All Rights Reserved 京ICP备08000853号-56 
京公网安备 11010802029508号 达内时代科技集团有限公司 版权所有
选择城市和中心
北京
黑龙江省
吉林省
内蒙古
河北省
陕西省
江苏省
湖北省
四川省
重庆
湖南省
江西省
贵州省
云南省
广西省
海南省
台湾